Tektites and Their Origin - Chapter Five

PHYSICAL PROPERTIES OF TEKTITE GLASS

The physical properties of tektite glass are interesting and significant in themselves, as well as in relation to theories of tektite formation.  This chapter is divided into: (1) mechanical properties, including acoustic properties; (2) optical properties; (3) electromagnetic properties; and (4) thermal properties.

The logic of putting the optical properties next to the mechanical properties, instead of with the electromagnetic properties of which they are really a part, is simply the close relation between specific gravity and refractive index, as well as that between polarization and strain.

The thermal properties include thermal coefficients of other properties.

MECHANICAL PROPERTIES

Specific gravity and porosity

The specific gravity of tektite glass ranges from about 2.21 for Libyan Desert glass (Clayton and Spencer, 1934) to more than 2.80 for the heaviest of the bottle-green microtektites (Glass, 1972b).Because of the existence of porosity in tektite glass, the most precise measurements must be made on crushed specimens.  However, Scheiber (1970) showed, by comparing with the refractive index, that the bulk measures of specific gravity are usually reliable within a few units in the third decimal place, unless there is obvious and conspicuous porosity.  Barnes (1939) finds total bubble volumes of 0.00023% and 0.15% for two bediasites.  This means that statistical studies can be made on the bulk specific gravity; it also gives a numerical measure of the freedom from bubbles of tektite glass in general.  This measure is significant when tektites are studied from the point of view of glass-making (Chapter 8).

The frequency distribution of tektite specific gravity at particular localities was studied by Chapman et al. (1964) who found that the frequency distribution of densities is markedly different at different points even in a relatively homogeneous area such as Australia.  On the other hand, they were able to use this method to relate some widely separated places such as southwest Australia with the Philippines, or Java with Charlotte Waters, Australia.  They found that the density histograms for points less than 100 km apart were generally indistinguishable, which gives an idea of the sharpness of the streaky structure of the Australasian strewn field.

King (1964b) studied the specific gravity of 329 bediasites.  His graphs show that in the southern part of the area, around Muldoon, the mean specific gravity is about 2.35, only a little higher than Georgia tektites (2.34); in the middle of the region it is 2.37; and in the north (Grimes County) 2.385.

Martin (1934b) made a large number of measures of specific gravity throughout the Australasian strewn field.  Baker and Forster (1943) measured specific gravities throughout Australia.  In particular, they found indications that for Port Campbell australites, the flange fragments had slightly lower specific gravity (2.387) than the body fragments (2.396). 

The specific gravity as a function of silica content is shown in Fig. 20.  It was noted by Tilley (1922) and later by Barnes (1939) that this relation is not precisely the same as the relation of silica content to specific gravity in terrestrial igneous glasses; the latter are lower by about 0.01 in specific gravity than tektites of the same silica content, presumably because tektites contain more of the heavy, divalent oxides, and less of the lighter, monovalent alkali oxides.

From Fig. 20 it is clear that the clan of the high-magnesium tektites and the bottle-green tektites is even higher in specific gravity than the general run of tektites, presumably because of the replacement of Al₂O₃, Na₂O and K₂O by MgO and FeO.

The equations of the three lines of Fig. 20 are each in the form:

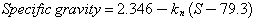
where k₁ = 7.73 x 10^-3; k₂ = 11.79 x 10^-3; k₃ = 16.07 x 10^-3; S is the silica content in weight percent.  The coefficient k₁ holds for the high-silica tektites; k₂ for the normal tektites; and k₃ for the high-magnesium branch. 

Note that almost all hand specimens of tektites as they are usually spoken of (without the Aouelloul glass, Darwin glass, microtektites, Libyan Desert glass, or the high-sodium variety) fall between a silica content of 68% and 82% along the line for normal tektites.

The problem of the relation of specific gravity to chemical composition has not been studied for tektites, although for commercial glasses it has been found (Morey, 1954, p. 221) that the reciprocal of the specific gravity, i.e. the specific volume, is approximately additive for glasses (that is, the specific volume of the glass is the weighted mean of the specific volumes of the constituent oxides).  It would probably be useful to compare calculated glass densities with observed densities, because the exact density of a glass depends both on its composition and on its heating history; see below.  To make the comparison, the specific volume is needed for FeO; it is not given by Morey.

Most wet-chemical analyses are accompanied by a more or less precise measurement of the specific gravity.  For the moldavites and the more silicic tektites these are well summarized by Rost (1972).  For tektites in the main range, the most important source is Chapman and Scheiber (1969).  For some australites, see Cuttitta et al. (1964); for indochinites and philippinites, the tables of Schnetzler and Pinson (1963, 1964a) are particularly useful.  For bediasites, Chao (1963) is the best source; for other North American tektites, see Cuttitta et al. (1967).  For Ivory Coast tektites, Chapman and Scheiber (1969) and Cuttitta et al. (1972) are the principal sources.  For the bottle-green microtektites, the source is Glass (1972b).

Hardness

Suess (1900) reports measurements of moldavite hardness on the corundum scale by Rosiwal; the hardness was 29.5 and 31 on two specimens, compared to 18.2 and 19.8 on two commercial glasses and 34, 35.6 on two obsidians.  On the more usual Mohs scale, the hardness is between 6 and 7 (Baker, 1959b); it approaches 7 for the most silicic tektites such as Darwin glass.  Bouška and Povondra (1964) measured microhardness on some moldavites with the Haneman apparatus; the results were from 900 to 1200 g/μm².  Weiskirchner (O'Keefe and Weiskirchner, 1970) finds that the hardness so measured decreases with load, increases with silica content, and shows significant mechanical hysteresis.

Strength

Centolanzi (1969) found that the ultimate tensile strength of tektite glass varies between 0.6 and 1.0 kbar (1 kbar is 10⁸ N/m²).

Elastic constants; acoustical wave velocities

Soga and Anderson (1967) tabulate the elastic constants for two tektites (see Table III).  They obtained the wave velocities by finding the resonant frequencies of small glass spheres; the other parameters are deducible (given the density) by standard formulas (Jeffreys, 1959, pp. 1-4). 

Table III: Constants of Elasticity

Surface tension

Chapman and Larson (1963) calculate from the table of Morey (1954, p. 206, table VII, 6) the surface tension of australite glass as 0.360 N/m (360 dynes/cm).

Crack formation; internal energy

Levengood (1966) measured the flaws which radiate from cracks in tektites, as in other glasses.  The length and number of flaws are related respectively to the internal energy and Young's modulus.  The flaws themselves might conceivably be the "mesh of small cracks" whose existence was postulated in Chapter 3 to explain the cross-sectional outline of the meandrine grooves.

Destruction by micrometeorite impact

Gault and Wedekind (1969) find that a tektite will be shattered if as much as 1 joule per gram is delivered to the tektite either by a single impact or by several impacts.  The figure is surprisingly low compared with the energy required to produce a crater of dimensions like a tektite in a semi-infinite solid.  The difference is due to the trapping of shock waves within the tektite body.

OPTICAL PROPERTIES

Refractive index

The refractive index, normally given as that of the sodium D line at 589.0 and 589.6 nm, and symbolized n_D,  is closely related to the specific gravity.  A similar plot has been prepared (Fig. 21) of n_D against silica content.  As with the specific gravity, three trends appear to be represented, each described by an equation of the form:

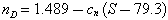
where c_n  has the value 0.001429 for the high-silica tektites, 0.002840 for the main range; and 0.003703 for the high-magnesium clan.

It follows  that the refractive index can be regarded as a function of the density, with the relations:

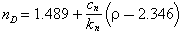
where c₁/k₁ = 0.1849; c₂/k₂ = 0.2408; c₃/k₃ = 0.2304.

Durrani (1971) found:

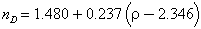
which fits reasonably well except for the high-silica materials.

Formulas exist (Morey, 1954) for the calculation of the refractive index from density and chemical composition.  They seem to work well for the more silicic tektites; at the silica content of the Ivory Coast tektites, discrepancies of the order of 0.01 are found between calculated and observed refractive indexes.

The refractive index varies considerably within individual tektites.  in typical splash-form tektites, the wavy structure (striae) corresponds to changes of 0.001 in the refractive index (E.C.T. Chao, quoted in Rost, 1972).  The waves have a physical thickness varying between 1 and 500 μm.  Barnes (1939) notes an individual bediasite (by no means typical) in which the index of refraction ranged from 1.483 to 1.512.  By contrast, in a group of 79 bediasites, the average index ranged only from 1.489 to 1.509.  Barnes later (1964c) found that at individual Muong Nong deposits (each of which may represent an individual block of incoming glass) the refractive index tends to vary by 0.010-0.015.  Rost (1972, p. 32) insists that even in moldavites, there is always a homogeneous basic vitreous substance which dominates in volume over the striae and other inhomogeneous parts.  Hubbard et al. (1956) note an australite in which the index of refraction varies from 1.504 to 1.524 over a small cross section.

The measurement of 1.538 for an individual moldavite from Senohrady by Novácek (1932) was discarded by Adamovska and Adamovsky (1967); it is not used here.  The silica content was 74.9%.

Dispersion

For Libyan Desert glass, measurements by Clayton and Spencer (1934) and for moldavites by Schwantke (1909) are shown in Table IV.

Polarization and strain

Although tektites are glasses, and hence never show strong effects in polarized light, yet they almost always show detectable birefringence resulting from strain; this is valuable as an indication of structure and history.  The discoveries of Wright, Barnes, Raman and others have been discussed in Chapter 4.

Table IV:  Dispersion in tektite glass

The ratio of birefringence to stress is the stress-optic coefficient, which is normally of the order of 3 brewsters (1 brewster is 10^-13 cm²/dyne, or in S.I. units 10^-12 m²/N).  Centolanzi (1969) measured the stress-optic coefficient of tektite glass.  His paper is obscure; it appears that he used a thin disk of glass of specific gravity 2.43, stressed by compression applied at two points diametrically opposite one another at the edges of the disk.  Using a standard formula for the stresses at the center of the disk, he found from his measurements a parameter Z, which he called the stress-optic coefficient, such that:

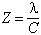
where  λ is the wavelength of the light; and C is the stress-optic coefficient as the term is generally used.  Centolanzi's stress-optic coefficient is 1/2  the quantity called the "fringe value of the material" by Frocht (1941, p. 159).  He found Z=177; taking 546.1 nm for the wavelength of the light, and allowing for the difference of units this implies 3.2 brewsters.

The numerical amount of the phase shift due to stresses was measured in some moldavites by Soukeník (1971a).  His units are nanometers of optical path difference per centimeter of path length (Morey, 1954, p. 167).  In S.I. units, Soukeník found strains averaging 10,000 (nanometers of optical path difference per meter of path length) but rising in one case to 55,500; ellipsoidal pieces tended to have about 20% less strain.  He found that strain increases systematically with size.  Obsidians, by contrast, show very little strain.

Soukeník's strains, using Centolanzi's stress-optic coefficient, would correspond to stresses of 3x10^-6 N/m² (30-180 bars). Hammond (1950) found stresses of 5x10^-6 to 8.5x10^-6 N/m² (50-85 bars) by similar methods.

Rost demonstrated (1972, p. 66) that when a strained tektite is broken, the strain reorients itself in accordance with the new shape of the fragment.  He denies that the figures seen between crossed polaroids can be used as an argument against the loss of the outer portions of the tektite (e.g. by corrosion).  Centolanzi (1969) puts the matter quantitatively; the reduction of the strain in a sphere to 20% of the initial value requires the reduction of the radius to 1/2 of the initial value.  Majmundar and O'Keefe (1967) found that the birefringence around the notches in moldavites can be made to disappear by annealing; if the specimen is reheated and quenched by an airblast, the strain reappears in the same pattern as before; and the strain around an artificial notch is indistinguishable from that around natural notches.  This means that the strain around the notches does not carry a memory of the way in which the notch was made; it is determined by the shape of the notch and the overall strain in the tektite.

Spectrum

The tektite absorption spectrum is shown in Figs. 22 and 23.  The absorption increases greatly toward the longer wavelengths.  The breaks between Fig. 22 and Fig. 23 and between the two curves of Fig. 23 each correspond to a scale increase (going toward longer wavelengths) by a factor of about 10.

Fig. 22 covering the range from 0.3 to 0.4 μm is redrawn from Stair (1955).  The ordinate is transmittance (transmitted light/entering light, I/I₀) for a bediasite (curve labeled 4) and an australite (curve labeled A), each about 0.5 mm in thickness.  The high ultraviolet absorption and the band at 1200 nm are due to FeO; the notch at 2800 nm is due to water (more exactly, OH) in the glass.  Libyan Desert glass has the same ultraviolet cut-off, but its transmittance is consistently high up to 4 μm.  Similar spectra in the region from 0.3 to 2.5 μm were found by Cohen (1958); Cohen plots the absorbance, A, given by:

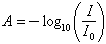
Gilchrist et al. (1969) obtained spectra similar to Stair's, and utilized the band at 2.7 μm to obtain the water content of tektites (see Chapter 6).

In the far infrared, from 4 to 7.5 μm, the curve is based on Perry and Wrigley (1967) who used a 65 μm thin section; from 7.5 to 24 μm it is based on Kadushin and Vorob'yev (1962), who powdered the tektites and put the powder between slabs of NaCl or KBr.  The particle size was less than 7 μm; this technique let them get some light through even this very opaque material.  Houziaux (1956) obtained a qualitative curve for this region.  He states that the fundamental vibrations of the silicon tetrahedron are at 8.5 μm (an inflection only in the observed curves), 9.5, 12.7, and 21.6 μm.  At 10.6 μm he notes a band in the long-wavelength wing of the band at 9.5 μm; this he attributes to oxides of alkalis or alkaline earths.

The reflection spectrum was observed by Perry and Wrigley (1967; see Fig. 24).  They found peaks at 457 and 1060 cm^-1 (21.9 and 9.4 μm)  which correspond to the chief depressions found in the transmittance by Kadushin and Vorob'yev (1962).  These are essentially the famous reststrahlen, or residual rays, of fused silica (Wood, 1934, pp. 516, 517).  Perry and Wrigley also found weaker bands at 77,000, 94,000, and 1,200,000 m^-1 (770, 940, and 1200 cm^-1), which can be seen in absorption in the curve of Houziaux.  By comparison with the  reflection spectrum of fused silica, they showed that the peaks at 45,700, 77,000, 1,060,000 and 1,200,000 m^-1 (457, 770, 1060, and 1200 cm^-1) were due to silica.  They further showed that the reflectivity between 60,000 and 90,000 m^-1 (600 and 900 cm^-1) is largely due to Al₂O₃.   In general, the reflectivity measurements appear to be considerably more expressive than the transmission measurements for wavelengths greater than 6 μm.

Emissivity

The maximum emissivity of tektite glass is given by Chapman and Larson (1963) as 0.91 for n=1.50.

Color

Most tektites are black; Georgia tektites and moldavites from Bohemia are various shades of olive green (Rost, 1972).  Moldavites from Moravia tend to be brown; however, this is a statistical rule.  There are light olive-brown bediasites from the Muldoon area (Barnes, 1951).  Aouelloul glass is yellowish-gray by transmitted light, and Darwin glass is gray.  Usually tektites show shades of brown or green, rather than gray, on thin edges; this helps to distinguish them from obsidians.  Thorpe and Senftle (1964) attribute these brown shades to submicroscopic spherules of Fe₂O₃ or metallic iron.

Microtektites are generally brown, black or yellow, or clear (Cassidy et al., 1969).  Among them, however, are the magnesium-rich bottle-green tektites.  These may have up to 0.2% Cr₂O₃ (Glass, 1972b) to which their color may be due.

It is puzzling that the "poisonous green" moldavites of Netolice (Bouška and Povondra, 1964) are rich in MgO, but not especially rich in chromium.  Morey (1954, p. 456) notes that the coloring effect of chromium in glass may depend on the other oxides present.

ELECTRICAL AND MAGNETIC PROPERTIES

In this section, the notation and units of Stratton (1941) are followed.  These are the same as the S.I. units used throughout this book.  The system is an MKS system in which the units have been so chosen as to eliminate factors of 4π in Maxwell's equations, at the cost of introducing them in the Coulomb equation and the analogous equation for the attraction of a magnetic pole.  For volts, amperes, and coulombs, the system is the same as the practical system, and very different from the cgs electromagnetic units generally used in scientific work.

Dielectric constant (specific inductive capacity)

In a non-ferromagnetic material such as tektite glass, when conductivity can be neglected, the specific inductive capacity ε/ε₀ (i.e., the permittivity ε, relative to that of free space, ε₀=8.854 x 10^-2 farad/m) is very nearly equal to the square of the refractive index.  It is the quantity called the dielectric constant; it is obtainable at optical frequencies from the data already given, and is about 2.25.

In the near infrared, Perry and Wrigley (1967) give the index of refraction, n (Fig. 25).  Here, however, the conductivity cannot be neglected; we have:

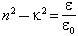
where  к is the imaginary part of the index of refraction; к is also graphed by Perry and Wrigley.

In the radiofrequency region,  the specific inductive capacity has been measured directly by Olte and Siegel (1961); they find 4.2 for the Libyan Desert glass, and 6.0-7.4 for some indochinites and australites.  A single moldavite gave 6.1.  The transition from values around 2.25 to values of 5 or more takes place at the frequency of the principal resonances, at 9 and 22 μm; it can be followed in the curves of Perry and Wrigley (Fig. 25).

Electrical conductivity

The electrical conductivity, σ, of tektite glass is related to the imaginary part, к, of the index of refraction by the equation:

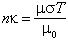
where T is the period of the vibration, σ the conductivity, μ the magnetic permeability, and μ₀ that of free space.  The ratio μ/μ₀ is effectively 1.  Hence the conductivity can be deduced from the curves of Perry and Wrigley for the frequencies corresponding to the resonance vibrations.

For lower frequencies, the resistivity (reciprocal of the conductivity) has been measured as a function of temperature by Hoyte et al. (1965) on synthetic glasses which simulate tektite composition.  At 300° C, the resistivity ranges from about 10¹³ Ωm (10¹⁵ Ωcm) in Hoyte et al.  (1965) for a moldavite, down to 3 x 10¹² Ωm for a javanite.  Their measures can be represented within 15% by the following formula:

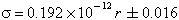
where r is the percentage of Na₂O in the analysis.  The unit here is mhos/m.

Magnetic permeability; magnetic susceptibility

The S.I. units are so chosen that the magnetic permeability μ₀ of free space is 4π x 10^-7.  The quantity which is called the permeability in the familiar cgs emu system is then equal to Stratton's specific magnetic permeability, μ/μ₀.  The magnetic susceptibility χ_m is given by:

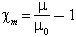
In practice, some authorities (Morey, 1954) use χ_m/4π, which is called the volumetric susceptibility.  Others, including those who have written on tektites, use χ_m/4πρ, where ρ is the specific gravity; unfortunately this may be called the specific susceptibility, though it is different from χ_m.  We shall call χ_m/4πρ the mass susceptibility.  Finally, some authorities (Hodgman et al., 1962) use the molecular susceptibility, Mχ_m/4πρ, where M is the molecular weight. 

It turns out that the mass susceptibility of tektite glass is generally less than 10^-5, so that μ/μ₀=1, with an error of less than 300 ppm; this justifies our previous assumption that the glass could be treated as non-magnetic in calculating the index of refraction or the dielectric constant.

Senftle and Thorpe (1959) found that the mass suceptibility χ_m/4πρ varies linearly with the iron content.  Their table 2 seems to be represented by the following formula:

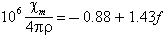
where f is the percentage of iron oxide, with all iron as FeO.  The unit of their table is emu per gram; the quantities resulting from the present units are numerically the same as those used by Senftle and Thorpe, but are dimensionless.  The chemical analyses which they used showed a considerable range in ferric/ferrous ratio, which was not reflected in the observed magnetic susceptibility; they suggested that in fact the iron is present primarily in the ferrous state.  Thorpe et al. (1963) drew similar conclusions from the analysis of bediasites; the data from their work is shown in Chao (1963); it suggests an equation of the form:

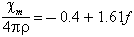
over the range from χ_m/4πρ = 3 to 8 with a scatter of only a few tenths in χ_m/4πρ.  In microtektites, Senftle et al. (1969) found a similar relation.

Magnetic intensity

Early investigations showed no detectable magnetic intensity in tektite glass, at the level of about 10^-4 emu/g.  (To convert measurements in emu/g to S.I., multiply by 10³.)  Booker and Harrison (1966) set an upper limit of 10^-7 emu/g.  De Gasparis et al. (1973) found evidence of natural remanent magnetism (NRM) in tektites of the Muong Nong type, although not in the splash-form tektites.  According to them, the intensity was between 10^-7 and 10^-6 emu/g.  The magnetism was blocked at 500-560° C (i.e. disappeared when the specimen was heated to this temperature).  They found that the magnetism could not be isothermal remanent magnetism (magnetism due to a brief exposure to a strong magnetic field) because it was much more stable against demagnetization by alternating fields.  They also found that there was no detectable change in the magnetism due to prolonged heating at 100° C, followed by cooling in a field of 1 oersted (about 80 A/m, in S.I.) which is the order of strength of the earth's field.  This, they felt, eliminated viscous remanent magnetism (a slow drift with time toward alignment with the earth's magnetic field) and chemical effects.  The behavior resembled that of thermal remanent magnetism (magnetism acquired by cooling from above the Curie point).  De Gasparis et al. conclude that the magnetism resulted from the cooling of the tektites in the earth's magnetic field, particularly because the angle between the layering and the direction of the magnetic field is at least roughly that which would be expected for Indo-China.

On the other hand, Nagata (1961, pp. 259-269) points out that there are at least theoretical reasons for believing that lightning could produce a form of remanent magnetism called anhysteretic remanent magnetism, with properties much like those of thermal remanent magnetism.  Although terrestrial lightning is observed to produce magnetism which is more easily erased than thermal remanent magnetism, Nagata's remarks indicate that lightning remains a possibility.  Note also that one of De Gasparis's specimens was more strongly magnetized than would be expected from the earth's magnetic field.

THERMAL PROPERTIES

Coefficient of thermal expansion (linear)

From the curve of Hubbard et al. (1956) one would scale a value of 40 x 10^-7 for the linear coefficient of thermal expansion between 100 and 500° C.  Chapman (1964) gives 7 x 10^-7 for silica, 29 x 10^-7 for a tektite with 80% SiO₂, and 42 x 10^-7 for a tektite with 65% SiO₂. Centolanzi (1969) gives 33 x 10^-7 for a tektite of specific gravity 2.43.

Hubbard et al. find that the rate of expansion diminishes markedly between 500 and 650° C; they identify 650° C as the critical temperature.  This temperature is more generally known as the transformation temperature, T_g (Jones, 1971).  It is believed that as glass cools from a melt, the atoms are at first able to rearrange themselves; but at the transformation temperature they lose this property; the arrangements then existing are frozen in, and further changes consist of a decrease in the oscillations around points, but not in further movement.  Since the transformation temperature is associated with the annealing process, it is important to note that Centolanzi (1969), presumably quoting measurements at Corning Glass, identifies the annealing range as 900-950° K, i.e. 630-680° C.  These figures are presumably for australites; for philippinites Heide and Brückner (1971) on other grounds find T_g to be in the range 850-950° C, while for moldavites they find that the transformation zone is from 900 to 1030° C; they support this by a study of the change of the refractive index.

Viscosity

For the viscosity, η, Chapman and Larson (1963) give for a tektite of 76% SiO₂, converted to S.I. units:

log  η = (27,620/(T-262)) - 10.09 [N sec/m²]

where T is the absolute temperature (1 N sec/m² is 10 poise.)  This is somewhat lower than the measurements of Volarovich and Leontieva (1939; see Fig. 26).  Friedman (1963) reports two measurements on a bediasite, plotted in Fig. 26. 

Hoyte et al. (1965) find that the activation energy for viscosity, E_η, is 3.65 times that for the electrical resistivity, E_ρ.  By measuring resistivity from 330 to 450° K, they were able to construct viscosity curves from 1370 to 1770° K.  From their work they concluded that the following formula represents the viscosity, η:

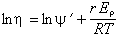
where ln ψ' is nearly constant for all tektites, r = 3.65, R is the gas constant, and T is the Kelvin temperature.  Numerically:

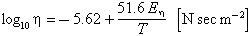
where E_η is the activation energy for viscosity in kJ/mol.  From the chart of Hoyte et al., it is clear that E_η varies  linearly with SiO₂ content, being about 277 kJ/mol (66.4 kcal/mol) for 70% SiO₂ and about 335 kJ/mol (80 kcal/mol) for 80% SiO₂.  Note that their equation 11 is in error; the coefficient of 1/T should be 10³ times larger.

Hoyte et al. point out that E_η is about 7.5 kJ/mol (1.8 kcal/mol) higher for annealed glass than for quenched glass.  Tektites are to be regarded as quenched.  The discrepancy between their values and Chapman's is approximately equal to the difference between annealed glass and quenched glass (Fig. 26).

The viscosity of Libyan Desert glass was found by Friedman and Parker (1969) to be almost six orders of magnitude higher than that of australite glass at the same temperature.  The activation energy is about 460 kJ/mol (110 kcal/mol).

Specific heat

The specific heat of tektite glass was found by Chapman and Larson (1963) for a Port Campbell australite with 76% SiO₂ to be:

C_p = 0.953 + 0.00025T - (27,000/T²) [kJ kg^-1 °K^-1]

Thermal conductivity

The thermal conductivity (Chapman and Larson, 1963) for the same kind of tektite as above was found to be:

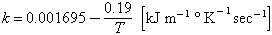
Time of cooling

Adams and Spreuer (1967)  calculated the cooling time for an opaque sphere in space, radiating to a vacuum, and having internal heat transfer by conduction.  The value of the thermal conductivity which they adopted was about 1/4 of that given above, so that allowance must be made in applying their graphs to the tektite problem.  This correction was made by Centolanzi (1969).  Earlier studies of the same problem were made by Watson (1935) and Greenland and Lovering (1962).

Vapor pressure

The vapor pressure of tektite glass was found by Chapman and Larson (1963) from mass-loss measurements as:

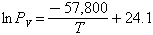
where P_V is in N/m² and T in degrees Kelvin.

Walter and Carron (1964) attempted to measure the vapor pressure by determining the boiling point of tektite glass as a function of temperature.  They found vapor pressures which, at the lower end of their range, near 1500°C, were approximately 10⁶ times higher than those of Chapman and Larson.  This work was criticized by Centolanzi and Chapman (1966) who redetermined the vapor pressure by a number of different methods, all of which led to the result that the vapor pressure is very nearly that given by Chapman and Larson, being:

ln P_V = (-57,400/T) + 23.50 [N/m²]

The results of Walter and Carron (1964) were apparently caused by the fact that tektite glass contains a small amount of volatile material, which forms bubbles at a temperature much lower than the boiling point of the majority of tektite material.  The work of Walter and Carron is valuable for questions involving escape of volatiles; but for determinations of vapor pressure, as this is needed for e.g. ablation calculations, the data to use is that of Centolanzi and Chapman (1966).

Heat of vaporization

From their thermal data, Centolanzi and Chapman (1966) determined a heat of vaporization of 11,900 kJ/kg, using the Clausius-Clapeyron relation.

Diffusion coefficients

The diffusion of gases in tektite glass was studied by Reynolds (1960); he found that helium should diffuse out of a typical tektite in 5 years;  neon requires about a million years; other gases, apart from hydrogen, require times much longer than available.  In accordance with these predictions, O'Keefe et al. (1962, 1964) found helium, and neon, but  not argon or nitrogen in tektite vesicles.  The helium and neon appeared to have diffused inward from the atmosphere.

The diffusion of metals in tektite glass was studied by Varshneya and Cooper (1969) and Varshneya (1970).  They were concerned with what is called the effective binary diffusion coefficient.  Their data yield the results shown in Fig. 27.  At 1800°C, the effective binary diffusion coefficient for iron in tektite glass is about 10^-11 m²/sec; that for silicon is about 1/3 as large.   These results are of significance in studies of the rate of homogenization of tektite glass.

Thermal variation of magnetic susceptibility

Thorpe and Senftle (1964) studied the variation of the magnetic susceptibility of tektites with temperature.  In addition to the variation to be expected if the susceptibility is due to ferrous iron, they found a temperature-independent component, which they attributed to the presence of about 30 ppm of  free iron or Fe₂O₃ in the form of submicroscopic spherules.  They attribute the brown color characteristic of tektites to the same spherules.

Thermoluminescence

Durrani et al. (1970) and Durrani (1971) have studied tektite thermoluminescence.  The phenomena are complex, and investigation has only begun.  An age (since last heating) of 0.7 (+0.24 / -0.19) million years has been found for indochinites.