THE TERRESTRIAL ORIGIN OF TEKTITES: ARGUMENTS AGAINST
In this chapter, the arguments against the terrestrial origin of tektites are presented. In particular, the arguments concern themselves with the hypothesis of origin by meteorite or comet impact. No other theory of terrestrial origin has been seriously put forward, except by McCall (1973), since the discovery by Chao et al. (1962) of nickel-iron spherules in philippinites. The chemical unity of the Australasian strewn field, from the western Indian Ocean east to Tasmania, and from Tasmania north to southern China, is evidence of origin from a single, relatively small region. No matter where (on earth) this source region may have been, the size of the strewn field demands a velocity of launch of at least 6 km/sec even if retardation by the atmosphere is ignored. This high velocity makes it difficult to believe in origin by terrestrial volcanic or cryptovolcanic explosions, as suggested by McCall, since the highest velocities for rocks from terrestrial volcanoes are believed to be about 600 m/sec (Sukhanov and Trifonov, 1974, p. 154). Theory (Oswatitsch, 1956) says that gases escaping from a confining chamber into a vacuum will not exceed a limiting velocity which works out at about twice the sound velocity in the gas. For water at magmatic temperatures, this limiting velocity is about 2 km/sec; the needed 6 km/sec is not physically attainable, unless the gas is heated to temperatures of 10,000° K or higher; and this greatly exceeds any volcanic temperatures. Hence the terrestrial origin of tektites is usually taken as meaning origin by meteorite or comet impact.
The discussion in this chapter is arranged according to the sequence of events in the hypothetical impact: the area before impact; the formation of tektite glass in the impact; the launch from the impact crater; the passage upward through the atmosphere; the passage downward through the atmosphere; and the final arrangement of the strewn fields.
PROPERTIES OF THE IMPACT SITE
If tektites are produced by meteorite impact, then it is hard to understand why the bottle-green microtektites are found in the three strewn fields for which microtektites have been found, namely the Australasian, the Ivory Coast, and the North American strewn fields. The composition of the bottle-green microtektites can be described as pyroxenitic; but pyroxenites are not common rocks. Daly (1933) examined 159,000 square miles (412,000 km2) of geologic mapping in North America; he found 5.7 km2 of pyroxenite, or a fraction amounting to about 1.4 x 10-5 of the total area. If one discounts the first occurrence of this material in the tektites, since any rock will have some pecularity, it remains true that the chances of two successive further occurrences is 2 x 10-10.
If tektites are the product of terrestrial meteorite impact, it is also puzzling that the particles of lechatelierite are persistently smaller than sand grains (Barnes, 1939). They average about 150 μm x 30 μm, and rarely exceed 1 mm in largest dimension, even when drawn out. Sand, on the other hand, is typically in the range of 200 μm diameter, ranging up to over 1 mm in diameter, even when it is approximately round.
THE GLASS-MAKING PROBLEM
As was shown in Chapter 6, the terrestrial material which most closely resembles tektites (chemically) is sandstone, such as a subgraywacke. Terrestrial igneous rocks, including almost all natural glasses, have the wrong composition. It follows that the production of tektites from terrestrial materials involves the formation of glass from rock which is not glassy, but consists of an aggregate of crystals. We are thus led to ask how glass can be made. We consider the process separately under the headings of solid, liquid, and gaseous state transformations.
Solid-state transformation
Meteorite impact sometimes transforms crystals into glass by a solid-state transformation. The end-result is called a thetomorphic glass (Chao, 1968) or or a diaplectic glass (Von Engelhardt and Stöffler, 1968). In a thetomorphic glass, the original crystal boundaries are retained; even the internal structure of the crystal may survive. The shock of the impact has disordered the crystal just enough so that it has become optically isotropic. Tektites are certainly not examples of thetomorphic glasses; if the original material was indeed crystalline then nothing survives of the original crystal boundaries, with the doubtful exception of the lechatelierite particles.
Liquid-state transformation
A violent meteorite impact may deposit so much heat in the target material that the material is transformed into a glass by the normal action of temperature and time. Shock theorists call such glasses normal glasses (Von Engelhardt and Stöffler, 1968). The transformation is accompanied by vesiculation (bubbling); there is flow, and the crystal boundaries are more or less completely lost.
The transformation of a sandy mass of crushed rock into a homogeneous and bubble-free liquid, which can then cool to what is ordinarily meant by glass, has been studied by glass scientists for many years. Three principal steps are involved (Cable, 1969, 1970). These are melting, refining (eliminating bubbles -- often called fining), and homogenizing.
Melting. As mentioned above, a violent shock can melt glass completely in a very short time. There is thus no obvious objection to the impact formation of tektites on this ground.
Refining. Terrestrial igneous rocks typically contain about 0.5% water; sedimentary rocks normally contain 1% water or more. Tektites, on the other hand, contain only about 0.01% water (see Chapter 6). If tektites are made from terrestrial materials, the water must be removed somehow.
One obvious possibility is that the water is lost by diffusion. However, it turns out (O'Keefe, 1964c) that loss by diffusion is much too slow, even for rather small tektites, and even at temperatures which are unreasonably high. For example, 100 seconds are required for a tektite 6 mm in diameter at 3000° K.
In the production of commercial glass the volatiles are sometimes not eliminated at all; instead, the bubbles are eliminated by raising the pressure until they dissolve. This cannot be the way that tektites are made, because, as mentioned, the volatiles in tektites have been lost, not just dissolved.
When the volatiles must be eliminated, the only known way is to allow bubbles to form and rise to the surface of the liquid.
If tektites are launched by meteorite impact, then it is clear that the bubbles cannot escape during the very brief time when the tektites are being accelerated by the forces resulting from the impact. Whether these forces are due to shock or to gas pressure, they can only accelerate the tektite by pressure. But under pressure, the gases will not come out of solution. The amount of water in tektite glass is so small that in order to make it escape by bubbling, it is usually necessary to reduce the pressure below atmospheric.
Following the launch phase, the tektites must move on a ballistic trajectory in free space from their origin to the point of fall. During this period, the pressure is low, and bubbles would be expected to form and expand. They would, in fact, be expected to convert the liquid to a foam, since the volume occupied by 1 g of water at 1200° C and atmospheric pressure is 6600 cm3. In 100 g of sedimentary rock, this steam would be accompanied by 99 g of liquid rock, which would occupy a volume of only about 45 cm3.
The bubbles would not escape, however, because during this period the effective value of gravity is zero; hence they would have no buoyancy. The problem of dealing with bubbles in a liquid which is in a ballistic trajectory is an important one whenever a liquid-fueled rocket engine must be stopped and restarted in orbit (Paynter, 1964). One must provide either a small "bottoming rocket" to accelerate the space-craft and so provide a g-force, or else one must comb the bubbles out with a mesh, or use some other ingenious device. None of these techniques appear applicable to the tektite problem, especially since tektite glass is exceptionally viscous.
The tektite will cool rapidly during the ballistic flight. Adams and Spreuer (1967) find that a sphere of diameter 2 cm will cool to the center in 100 seconds, at least in the sense that the central temperature will be below 1200° C, and hence the viscosity very high. The flight time exceeds 100 seconds for flights of only 65-km range (Hawkins and Rosenthal, 1962). Hence the gases cannot escape after flight.
It can also be shown (O'Keefe, 1964c) that regardless of the viscosity of the tektite, any program of acceleration which will force the bubbles to the surface will also reduce the liquid mass to a cloud of fine droplets. Both processes involve the same non-dimensional number (the Jeffreys number, equal to the ratio of the Reynolds number to the Froude number).
Friedman and Parker (1969) calculated the rate of escape of bubbles from liquid Libyan Desert glass. At 1600° C, they found that, under terrestrial gravity, escape through 2 cm of glass requires about 47 days. Note, however, that at this temperature, in a vacuum, the glass evaporates at the rate of 2.9 x 10-5 cm/sec. Hence the supposed 2-cm layer will evaporate in less than 1 day, or long before the bubbles escape. The same will then be true at all higher temperatures, because both viscosity and evaporation can be thought of as following an Arrhenius-type law (like those on p. 112 [typist's note: "p. 112" signifies in the print edition Chapter 5, subheadings "Specific heat" to "Vapor pressure"]) and the coefficient of -1/T for viscosity is slightly lower than that for evaporation, and hence the change with temperature is slower. (Note that Friedman and Parker's extrapolation to higher temperatures does not follow the Arrhenius law, for unexplained reasons.) This difficulty (being unable to fine the glass before it evaporates) is well known in the industrial production of silica glass (Winship, 1954).
As would be expected from these considerations, most normal (non-thetomorphic) glass from meteorite impacts is vesicular. Some (Chao, 1963) is dense, and has somehow retained most of it water. It is possible in principle at least that impact glass which is sufficiently densely buried in a layer of hot throwout should lose its volatiles by diffusion. But the hypothesis of the instantaneous formation of dense, water-free glass from ordinary sandstones, in material which has never been deeply buried, seems to be indefensible.
Homogenizing. The third problem of glass-making is that of homogenization. The word glass can in principle mean any amorphous material; but in commercial glass it implies a material which is also homogeneous on a molecular scale; and tektites are glasses in this sense also. To reach this homogeneity demands diffusion, which is a slow process in viscous liquids. Numerical calculations require the coefficient of diffusion; unfortunately, in real glass-making problems, many components are simultaneously diffusing into each other, so that the concept of the diffusion coefficient loses its meaning. For some purposes, however, it can be replaced by the effective binary diffusion coefficient, a concept developed by A.R. Cooper. This can be applied, with some care, to give the rate of diffusion of a metal with respect to the glass as a whole.
Actual values of the effective binary diffusion coefficients for iron and for silicon in tektite glass were obtained by Varshneya (1970); these results are shown in Chapter 5. Varshneya and Cooper (1969) used the iron data to calculate the time required to homogenize the glass of a Thailand tektite. They concluded that even if the initial material was arranged in alternate perfect laminae, of iron-rich and iron-poor material, each pair of laminae having a thickness of 40 μm, homogenization would not occur within a reasonable time (a second or so, for impact).
Let us consider a more realistic case. A typical sandstone will have a framework of sand grains (Pettijohn, 1957), usually having a mean diameter greater than 125 μm. These will include grains of quartz (SiO2), feldspar and other minerals. There should be not over 15% of fine-grained matrix, if the sandstone is a subgraywacke, as suggested by S.R. Taylor (1966). Pettijohn further finds that in the range of 125 μm, over 90% of the grains are monomineralic (composed of a single mineral).
We suppose the whole mass to be shock-melted. Then the dissolution of the quartz grains (for example) demands diffusion of silicon through distances of the order of 1 grain diameter as a minimum.
But this is not enough, because even after the grains have disappeared, the resulting mass will be inhomogeneous because of statistical variations in the relation of quartz to the other constituents in the initial sandstone. We can consider the problem as if the effect of diffusion were to average the composition of all the grains in a certain volume. Suppose the volume contains 100 sand grains. If we calculate the normative mineral composition by the standard methods, we find 45% quartz and 55% of other minerals. Then on the average, 45 grains out of the hundred will be quartz. The actual number expected is given by the binomial distribution, whose standard deviation σ is given by Fry (1965, p. 222):
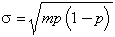
where m is the number of grains, and p the fraction of quartz grains. We find at once that σ is very nearly 5.
Hence if diffusion takes place only through batches of 100 grains or so, then we can expect a standard deviation of the silica content which will correspond to adding or subtracting 5 quartz grains to the mean value of 45. Since there is about 50% silica in the non-quartz grains, this works out to a standard deviation of 2.5% in the total silica content.
In fact, however, the graphical presentations of Walter (1965) show that the standard deviation of the silica content even in a Muong Nong tektite may be only 1%. Hence if tektites are the result of the melting of sandstones, we must consider that diffusion takes place through larger volumes; with 1000 grains the expected standard deviation is reduced to 0.8%, which is a reasonable approximation to the observations of Walter.
It follows that diffusion is called upon to reduce the irregularity in composition in a sphere of diameter 1.25 mm (i.e. 1000 grains of diameter 125 μm) to, say, 1/e of the original amount; we next show that this demands an excessive time.
As usual in calculations of diffusion, we make use of the fact that the diffusion of matter is mathematically like the diffusion of heat. From the thermal calculations of Carslaw and Jaeger (1959, p. 234), we see that the diffusion into a sphere requires that:
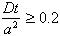
where D is the diffusion coefficient, a the semidiameter of the sphere, and t the time. Substituting D=3x10-8 cm2/sec from the curves of Varshneya (Chapter 5), for 1800° C, and a=0.062 cm, we find that a time of 2.6x104 seconds, or 7.2 hours would be required for homogenization.
It might be imagined that the process of homogenization could be aided by mixing. The effects of mixing can indeed be very powerful in speeding-up homogenization. Consider, for instance, a rod of glass, divided lengthwise into a red half and a green half. If the rod is now heated, stretched and folded in two, and reshaped, it will have two red and two green stripes. If we stretch and fold again, there will be four of each, and so on. After 20 steps, the separate red and green portions are reduced to a millionth of their original thickness.
Something of this nature, though not nearly as effective, clearly occurred with many splash-form tektites, in which the lechatelierite particles are drawn out into filaments 20 times as long as they are thick.
The data on homogeneity quoted above from Walter (1965) is for Muong Nong-type tektites, however; in these, the lechatelierite particles are nearly equant (i.e., have nearly equal diameters in all directions) and lack the long tails of the lechatelierite in the splash-form tektites. It follows that we cannot explain the homogeneity of the Muong Nong tektites by a mixing process.
Further evidence against mixing in the Muong Nong tektites is furnished by the layering, which is usually not strongly contorted.
If the temperature in the Muong Nong tektites has been very high, then the diffusion could have occurred more rapidly. On the other hand, Walter (1965) reports crystalline quartz and coesite in the same material as that used for the study of homogeneity. Temperatures above 1800° C would destroy both minerals in a few minutes or less. Similarly the presence of other crystalline materials in tektites (Glass, 1970c) speaks against high temperatures.
Finally, the spinous voids (see Chapter 4) found in many Muong Nong tektites would collapse into spheres or ellipsoids because of surface tension if Muong Nong tektites had ever been soft. O'Keefe (1966b) calculated that the time required for homogenization would be approximately 107 times greater than that required for the collapse of the spines. Since the diffusion time is roughly proportional to the viscosity, by the Einstein-Eyring relation, it follows that this discrepancy cannot be removed by altering the assumed temperatures.
From the experimental point of view, Varshneya and Cooper (1969) heated one artificial tektite batch for 24 hours at 1550° C; it still had bubbles. Another batch was heated at 1550° C and then had a 4-hour soak at 1800° C; this batch was bubble-free. Neither batch was as homogeneous as a Thailand tektite.
Note that in a vacuum the tektite would evaporate in 4 hours at 1800° C. Moreover, the activation energy for iron diffusion is much below that for vaporization (64 kcal/mol versus 180) and hence vaporization would, in a vacuum, precede homogenization at all higher temperatures.
In short, the idea of producing homogeneous glass by instantaneous heating of natural sandstones fails by many orders of magnitude.
Transformation in the gaseous state
Could tektite glass be formed by evaporation and recondensation? Something of this kind occurs in an atomic explosion, in which large quantities of silicates vaporize and then condense. The process could well be imagined to eliminate water and argon, and to result in a homogeneous glass. The difficulties in accepting this idea are as follows:
(1) When silica is evaporated and then recondensed, the result is not stoichiometric SiO2 unless the process is carried out very slowly, at the lowest possible temperatures. Hass et al. (1969) describe the evaporation and recondensation of SiO2; use is made of an electron gun, defocussed to avoid overheating and decomposition. Films so produced are transparent; but if evaporation is done using a focussed beam, or a directly heated boat of some refractory material, then the deposited film is overheated and decomposed. Non-stoichiometric silica has strong absorption bands, especially to the violet of 450 nm (Cox et al., 1964). Sinclair and Peters (1963) describe similar techniques, and note deposition rates of 7.5 nm per minute. To build a layer 1 cm thick at this rate would require several years.
The basic difficulty is that in the gaseous form, silicon dioxide decomposes:
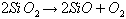
The equilibrium constant is given in the JANAF tables (Stull and Prophet, 1971); in the presence of atmospheric oxygen the ratio of the two molecules is as in Table XVII. Serious decomposition of SiO2 sets in above 1400°
K. Clearly, if allowance is made for the very low PO2 found by Walter and Doan (1969) the ratio of SiO/SiO2 will be still higher.
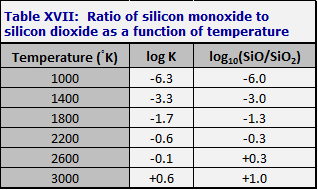
The blackness and opacity of non-stoichiometric silica is in obvious contrast with the optical properties of Libyan Desert glass and the Georgia tektites and moldavites.
(2) The recondensation process would be expected to begin with the more refractory oxides, and end with the most volatile. As a result, it would be expected that the microtektites would have an outer coat rich in the more volatile oxides. Such coats (rich in lead and iron) are actually observed on atomic fallout (Norman and Winchell, 1966); but nothing of this kind is seen in tektites, although it has been looked for (B.P. Glass, personal communication).
(3) It is essential to the hypothesis of terrestrial impact that the tektites should be distributed by expanding gases formed during the impact. But the gas expansion itself insures that lumps of condensing glass will not grow to large size (compared to nuclear fallout, i.e. microgram size) before the cloud becomes so dilute that growth ceases (Stewart, 1956).
(4) The Muong Nong tektites in particular possess a horizontally layered structure, which probably formed on some planetary surface, because there is a definite orientation of the vector of remanent magnetism with respect to the layering, and because there is evidence of welding of small particles. The welding could not have taken place after the arrival of the glass at the surface of the earth, because Muong Nong tektites, like other tektites, are never welded to true terrestrial materials (such as sand, loam, or crystalline rock of the earth).
Observations of impact glass versus tektites
From the observational standpoint, it is indeed found that tektites differ from impact glasses (see Plate 20) in that they are more homogeneous and less vesicular, and that the dense impact glasses have not lost their water content. These points were brought out by Chao (1963); and indeed the above discussion of the glass-making problem can be considered as no more than an attempt to provide a theoretical foundation for Chao's observations.
The instantaneous production of substantial masses of homogeneous and relatively bubble-free glass from common soil and rocks is not physically comprehensible, and has not been observed.
ARGON LOSS
As pointed out in Chapter 7, the process of expelling argon from tektite glass is extraordinarily difficult; it demands, in effect, the complete volatilization of the tektite. It does not seem plausible that the argon could be expelled in a terrestrial impact in a matter of a second or two. But if this cannot happen, then why do tektites yield good K-Ar dates? Shock alone has little effect on the argon distribution; it is well-known that in lunar rocks the K-Ar dates are almost always very old, although at least some lunar rocks must have been recently shocked by impact.
DEFICIENCY OF VOLATILES
As compared with terrestrial rocks, tektites are systematically deficient in elements which are volatile at temperatures of 1000°
C and below. This
point was noted in Chapter 6. The deficiency is qualitatively similar to the deficiency noted in lunar rocks. Comparison of terrestrial impact glasses with their parent rocks (S.R. Taylor, 1966, 1973) shows no similar pattern of loss.
LAUNCH PROBLEMS
One of the great surprises if the Apollo and Luna programs was the finding that the impact of meteorites on the moon has sent no identifiable materials to the earth. No meteorite and no tektite found on the earth's surface corresponds in composition to the typical lunar rocks of the maria and the highlands. Anders et al. (1971) remarked, in their study of Apollo 12 material, that "the now-established absence of lunar rocks in the world's meteorite collections apparently rules out an origin from larger bodies (Mars, Mercury, etc.) because ejection of rocks by impact is apparently very improbable even for the moon, whose escape velocity is as low as 2.4 km/sec." Of course no one knows whether meteorites or tektites correspond to some rare class of lunar rocks; but to establish Anders' conclusion it is enough to say that they do not correspond to the common types of lunar rock. Impact ejection, unlike volcanism, is a random process.
The above conclusion, that impact cannot produce velocities over 2.4 km/sec, is strengthened when we note the rarity of the petrographic marks of shock in the large rocks of the lunar surface. In the soil, on the other hand, shock is relatively common.
Again, at any point on the moon it is found that the decimeter-sized specimens are all of a single type, or a small range of types. These are believed to be the same as the underlying rock, although bedrock was seen only in Apollo 15. The range of rock types is much larger in the soils. Even among the soils, however, it is uncommon to find particles which have clearly been sent long distances by impact. Exotic particles tend to belong to a few types, such as the green glass spherules, or the orange spherules, for which the possibility of volcanic activity could not be ignored.
The underlying cause for this failure to eject particles with high velocity from impacts has been discussed by Öpik (1958b). In a shock, there is an unavoidable connection between shock pressure p and shock velocity w, of the general form:
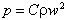
where ρ is the density and C is a dimensionless constant of order of 1. As soon as the velocities approach the lunar escape velocity, the corresponding pressures approach 20 x 109 N/m2, or about 200 kbars. A rock can survive a pressure of this size if it is confined on all sides; but in that case it cannot be launched. If it is to be launched, the pressure must be one-sided; then the rock will be crushed to powder.
If the pressures are a little higher, the rock will be liquified and sprayed. It will not be launched either as a solid mass or as a gob of considerable size.
Evidently, if impact cannot produce velocities of 2.4 km/sec or larger, it is still less likely to produce the 4 km/sec required to explain the North American strewn field, or the 6 km/sec required to explain the Australasian field, even in the absence of atmospheric resistance.
Many tektites have obviously been shaped by surface tension, or forces no stronger; this is indicated by their external shapes, and made certain by the presence, in some tektites, of internal bubbles which are nearly spherical and approach a centimeter in size. Such an object would be destroyed, literally, by a breath (Chapman and Larson, 1963). A terrestrial impact event capable of launching the object at 6 km/sec would necessarily involve one-sided pressures of about half a megabar (5 x 1010 N/m2).
It was suggested by Lin (1967) that this argument of Chapman did not take into account the effects of viscosity. However, we note that the high pressures come when the tektite is hot; if it is sufficiently viscous to resist deformation at this time, then it turns out from a numerical analysis that it cannot be sufficiently fluid later on, when cooler, to yield to surface tension (O'Keefe, 1963).
UPWARD PASSAGE THROUGH THE ATMOSPHERE
Even if a tektite were to be launched upward at the very high velocity demanded to reach the outer parts of the strewn field, it could not penetrate the undisturbed atmosphere. It is well known that meteorites weighing less than several hundred tons always reach the earth with terminal velocity (a few hundred meters per second or so) rather than with their velocity in space (not less than 11.2 km/sec). This point was first made by Nininger (1943b); later it was discussed by Chapman and Larson (1963), and Adams (1963). Lieske and Shirer (1964) calculated atmospheric trajectories for tektites; a 1-g tektite moving at 11.2 km/sec will be arrested after 360 m at flight at surface atmospheric density.
The basic problem is that a tektite moving through the atmosphere is preceded by a shock wave, also traveling at a speed of, say, 25 times the velocity of sound. Behind the shock wave, the air moves with subsonic velocity with respect to the tektite. This means that with respect to the ground, the mass of air, dM, behind the shock, has got within a few percent of the velocity, V, of the tektite. The momentum which it has gained, namely VdM, must equal the momentum lost by the tektite, namely, -M0dV, where M0 is the mass of the tektite:
VdM = -M0dV
Let V0 be the initial velocity of the tektite, and Vs the velocity of sound; then:

The integral on the left is approximately the column integral of the airmass encountered by the tektite; call this M1. Then:
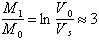
i.e. the tektite will be reduced to terminal velocity when the column integral of the air encountered is about three times its own mass. For a tektite with a frontal area of 1 cm2 (10-4 m2 ), passing vertically through the atmosphere, this integral is close to 1 kg; it is thus hundreds of times too large to be overcome by the tektite's momentum. The derivation is not precise, but it makes clear the fact that the difficulty is not some aerodynamical subtlety, but is a manifestation of Newton's Third Law, plus the fact that air pressure on the rear surface of the tekite is negligible at hypersonic speeds.
The whole problem is, of course, made two orders of magnitude more difficult by the finding that microtektites cannot be explained as ablation products of microtektites; they seem to have arrived as separate bodies.
In reply to these arguments, Cohen (1963) suggested that the explosion resulting from the impact produced a local vacuum, through which the tektites penetrated the atmosphere. Lieske and Shirer (1964) replied that the partial vacuum so produced would still have a density so high as to stop the tektite; further, they noted that the blast wave is not likely to penetrate the whole atmosphere.
Hawkins et al. (1964) offered an ingenious solution to this problem. They suggested that the dust and rock from the explosion, which should greatly outweigh the melt, would burst through the atmosphere and open a path for the tektites by driving the air before them. If this explanation were correct, then the tektites should have been accompanied by large volumes of dust and sand. On land, of course, these deposits might well be unnoticeable. B.P. Glass tested this idea by making counts of sand grains in a core which also contained microtektites. The results are shown in Fig. 42; there is no increase in sand near the time of microtektite arrival; hence this idea, which deserves more attention than it has had, does not work. It seems probable that in any kind of terrestrial impact there should have been great masses of partly fused rock; but nothing is noted in the oceanic cores.
The problem was further discussed by Lin (1966), who considered that the air might move along with the tektites. Lin perceived that if the tektite outruns the blast wave from the impact, it will reach undisturbed air, and will be stopped, as mentioned, unless the air is of very low density. The velocity of a shock wave (unlike that of a sonic wave) depends on the strength of the shock; it diminishes in proportion to r-3/2, where r is the distance from the explosion. However, for the part of the shock wave that goes vertically upward, there is a counteracting influence; a negative density gradient increases the shock velocity. For an explosion which greatly exceeds 2x1017J (i.e. 50 megatons TNT equivalent) the atmosphere blows out at the top for this reason. This blowout is necessary for the escape of tektites into ballistic orbits in empty space. The critical energy Lin designated E*.
However, matter rising vertically from the impact cannot be expected to contain solid or liquid particles; there will be only gases from the impact. Hence, Lin argued, the only explosions capable of launching tektites are those which are so violent that the gases move outward horizontally (so that they can entrain surface matter). Because of the curvature of the earth, the waves which start out at a tangent to the earth's surface eventually escape into the very high atmosphere; the tektites entrained can go on into space.
The energy demanded is 106 E*, or 2 x 1023 J. The corresponding crater dimensions, using the theory of Bjork (1961) are 300 km diameter, and 40 km depth.
Lin's paper was discussed further by Chapman and Gault (1967a). After making a number of corrections, they concurred that an explosion of the type contemplated by Lin, producing a crater 280 km in diameter, would be capable of ejecting solid matter into space. They pointed out that the Ries crater is about 103 times too small, and Bosumtwi about 103 times too small; they felt that it was doubtful that such a huge crater as required could be concealed anywhere on earth.
Lin (1967) replied that the mechanism which he had discussed was not applicable when the range was as short as that from Bosumtwi to the Ivory Coast tektites (300 km to the grouping near Ouellé known at that time) or from the Ries to the moldavite strewn field. Glass (1968) showed, however, that the Ivory Coast strewn field extends to a distance of 1600 km from Bosumtwi when he found microtektites off the coast of Liberia which were later shown to be chemically part of the Ivory Coast strewn field. The density of microtektites in this single ocean core and the indicated size of the field are such that a simple calculation suggests that the total mass of the Ivory Coast strewn field is not necessarily significantly inferior to that of the Australasian strewn field (B.P. Glass, personal communication).
For the North American strewn field, Glass et al. (1973) find that the suggested mass, on the basis of four cores, comes out three orders of magnitude greater than that of the Australasian strewn field. This, however, appears to be a mistake (B.P. Glass, personal communication, 1975); it is about one order of magnitude greater.
It is thus hard to accept the hypothesis of the terrestrial origin of tektites if we believe Lin's theory. It seems to call for two Pleistocene craters, of which one at least has an area about like Ireland, and a volume about like the land surface of Antarctica above sea level. In addition, a third crater, of Tertiary age, is called for which is ten times as effective in producing tektites. Craters of this size and this recency ought to be discoverable.
A somewhat different theory for terrestrial origin has been developed by David (1966a, b, c, 1967a, b, 1969, 1972). David notes that the physical evidence precludes a slow cooling process for tektite glass, and concludes that the shock produced by the impacting meteorite could not have left much residual heat in the tektites. Since shock processes normally leave behind something like half the heat developed at the peak of the shock, David chose a theory which depends on not shocking the tektite material. He considers that the source material was the layer of compressible soil just at the surface of the earth. Because of its softness, the effect of impact pressure was not to shock the soil, but to produce isentropic compression (i.e. compression without change of entropy, and hence reversible). During the subsequent expansion, the heat produced by the compression is turned back into mechanical energy; i.e. the process is efficiently reversed. This could happen only in the very thin zone between the shock wave which propagated downward into the earth and that which propagated upward into the meteorite. His calculated pressures go up to about 8 Mbars (8 x 1011 N/m2) and are released after about 100 milliseconds.
It is essential to this theory that tektites be made from the top meter of the earth. For a total mass of 109 tons, as required for the North American strewn field, a circular area of 5 x 108 m2 must be stripped; this means that the impacting asteroid must have had a diameter not less than 25 km. The crater which would be excavated would have a diameter approaching 100 km (Chapman and Gault, 1967a). This is an unreasonable size for a Tertiary crater in North American of which no trace can be found.
David's theory was constructed before the mass of the North American strewn field was known. Even at that time, however, he very properly pointed out that the derivation of tektites from terrestrial impacts required an "a priori incredible process" which could be justified only by what he felt to be the weight of the geochemical evidence. It is for this reason that the discussion of physical theories of tektite formation has been postponed to the chapter on arguments against the terrestrial origin of tektites.
Vand suggested (1966) that tektites were formed by jets of liquid material which resulted when a cavity in the earth (formed by the arrival of a meteorite) collapsed after the impact. The jet would have enough mass back of each square centimeter of frontal area to drive through the atmosphere. It would explain, he felt, the strewn fields like the moldavite strewn field and the Ivory Coast strewn field, which subtend only a small angle at the initial crater.
This idea was considered by Adams (1965) who showed, from considerations of hydrodynamics, that such a jet would necessarily be strongly retarded; to reach a height of 200 km with a velocity of 1 km/sec an initial velocity of 74 km/sec is necessary. Moreover, the jet breaks up into droplets which are themselves destroyed. Finally the jet sheds liquid drops all along the line over which it passes.
Adams further found that the jet could not go back into the hole in the atmosphere made by the incoming meteorite because this hole would close up promptly as a result of the heating of the air.
STREWN-FIELD GEOGRAPHY
If tektites were the result of terrestrial impact, it would be expected that they would be arranged in streaks radiating from the crater of origin. Near the crater of origin, one would expect a greater abundance of tektites.
In fact, in the Australasian strewn field, the streaks are subparallel to one another (Fig. 10). They do not radiate from any point within the strewn field, nor is there any conspicuous concentration anywhere.
In the moldavite strewn field (Fig. 13) there is a distinct suggestion of two parallel streaks of slightly different composition, running NW-SE, i.e. nearly perpendicular to the direction of the Ries crater. The impression is reinforced by the fact that in each region, the heaviest tektites are at the northwest end of the streak. The new tektites found at Prague support this pattern.
Although Vand (1966) suggested that the moldavites are the locus of a jet from the Ries, there are no moldavites near the Ries. The new Prague tektites increase the angle subtended at the Ries from 15° (Cohen, 1963) to 26°, which weakens the concept of the field as a single radial splash from the Ries.
Similarly the finding of microtektites off the Liberian coast increases the angle subtended at Bosumtwi by the Ivory Coast strewn field from 12° (Cohen, 1963) to 49°.
DOWNWARD PASSAGE
The pattern of ablation observed on flanged australites is found (Chapter 3) to imply entry velocities greater than those expected for objects flying from point to point on the earth. The pattern is consistent with velocities in the range of 8 km/sec only if the angle of entry is very nearly horizontal, and if we set aside the evidence from ringwaves and flange shapes, and from the thickness of the zones affected by heating.
It has been informally suggested from time to time that the same ablation phenomena might be produced by gases blowing upward past a tektite, and so accelerating it to its flight velocity. But Chapman et al. (1962) showed that australite shapes are stable only if the australite is in descending hypersonic flight, i.e., flight in the direction of increasing density. If moving in the direction of decreasing density, australites would be expected to tumble so that there would be no difference between the anterior and the posterior sides.
The credibility of the re-entry theories which are being used here is enhanced by the fact that more or less similar theoretical studies underlie the heat shields in use for many missiles and spacecraft.
CONCLUSION
The ci-devant Comte de Fourcroy (Fourcroy, 1804), considering the evidence for the cosmic origin of meteorites, remarked, "In such a question, one is compelled to choose between ideas which are just as unprecedented, the one as the other; and it is only by eliminating the absurd or the impossible that one is forced to accept what would at first have seemed almost unbelievable."
It is absurd to suppose that impacts of large objects take place preferentially on very rare pyroxenite rocks, or that the earth has a number of undiscovered Cenozoic craters larger than Ireland, or that the standard re-entry calculations contain gross errors leading to underestimates of the ablation. It is impossible to make good glass, devoid of water, instantly from common rocks and soil, or to drive argon out of tektite melts instantly, or to launch megascopic particles at 6 km/sec by shock, or to penetrate the atmosphere with gram-size bits of glass at hypersonic velocities.
We are thus forced to accept the conclusion, which at first seems incredible, that tektites, despite their remarkable resemblance to terrestrial rocks, do not originate on the earth.