ISOTOPES, FISSION TRACKS, AND COSMIC RAY TRACKS
INTRODUCTION
The most important application of isotopic analysis in the tektite problem to date has been the discovery of the ages of the strewn fields. Since fission-track analysis leads to similar (and, fortunately, concordant) results, the fission-track methods of age measurement are described together with the isotopic age measurements.
Isotopic analysis has also been used to test for effects of primary cosmic ray bombardment, such as is detected in meteorites. Here again the track methods reach the same result, and are described together with the isotopic methods.
Isotope studies of deuterium/hydrogen and the stable isotopes of oxygen and silicon are of importance in identifying possible source material for tektites.
ISOTOPIC AND FISSION-TRACK EVIDENCE CONCERNING TEKTITE AGE
The amount (in numbers of atoms) of any radioactive parent nuclide P,after a time t is given by: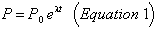
where P0 is the initial amount of the parent material, and λ is the decay constant, which is related to the half-life T½ by:
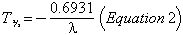
The amount in numbers of atoms of any daughter product D is given by:
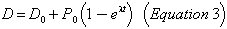
where D0 is the initial amount of the daughter product.
The reader is warned that in many discussions of radioactive processes, the equations are apt to be written so as to give the unknowns, P0 and D0, from the known quantities; this is how the experimenter sees the problem. We are here chiefly interested in the results, and have therefore used this more obvious way of looking at the relations.
Potassium-argon method
The decay of 40K to 40Ar (by electron capture) gives a method of determining the age of a rock since the time when it was last thoroughly outgassed. In principle, one collects the argon by heating, allows for atmospheric argon (which contains 36Ar; the radiogenic argon is pure 40Ar), and compares with the total potassium, assuming that 40K is 0.0118%, and using appropriate values for the decay constant and for the side production of (useless) 40Ca.
The important point is the heating required to remove the argon. H.E. Suess et al. (1951) heated tektites to 400°C; they obtained only upper limits to the ages. Gerling and Yaschenko (1952) also obtained only upper limits, including a limit of 3.1 million years for the moldavites. Gentner and Zähringer (1959, 1960) obtained values of 0.53-0.69 million years for the Australasian tektites, and 8.5-8.9 million years for moldavites. They commented that Gerling and Yaschenko probably had not heated the moldavites strongly enough; they recommended 15 minutes at 1800°C. Reynolds (1960) obtained ages up to 0.80 million years for the Australasian tektites, 13.5 million years for the moldavites, and around 30 million years for North American tektites; these results were substantially correct. Next, Gentner et al. (1961), referring to Lippolt's dissertation, raised the age of the moldavites to 14.7 million years, in agreement with Reynolds and with their own values for the age of the impact glass from the Ries Kessel; it is clear that their earlier moldavite ages were themselves in error as a result of incomplete outgassing. The same authors recommend (1963) that the sample be evaporated. Signer (1963) found that he could not extract all the argon by heating for 6 hours at 1800°C; he needed 20 hours at 1800°C or 2 hours at 2000°C. He remarked that there is no conceivable way by which such outgassing could have occurred in space; the potassium would have been lost with the argon at high temperatures. Schaeffer (1966) and McDougall and Lovering (1969) reiterate the need for complete vaporization to get out the argon. Schaeffer comments that the difficulty is connected with the lack of volatiles in tektites; in the absence of volatiles, bubbles do not form. In this case, as Signer remarks, gases must reach the surface by diffusion, which requires an inordinate amount of time.
The point is of considerable theoretical interest. Tektites normally yield ages which are concordant with each other and with the stratigraphic age of the materials in which they are found. It seems to follow that they were thoroughly outgassed near the time of their arrival at the earth. In the case of the Ries and Bosumtwi glasses, the outgassing might have occurred while the glass was buried in a hot deposit of throwout; argon will diffuse out of rocks at moderate temperatures if very long times are available. On the other hand, rocks which cool in flight are found to lose only part of their argon (Hartung et al., 1971); thus it is difficult to explain the argon loss for tektites if they are formed by meteorite impact on earth. Among known impact glasses, careful selection is required to find glasses which have been thoroughly outgassed.
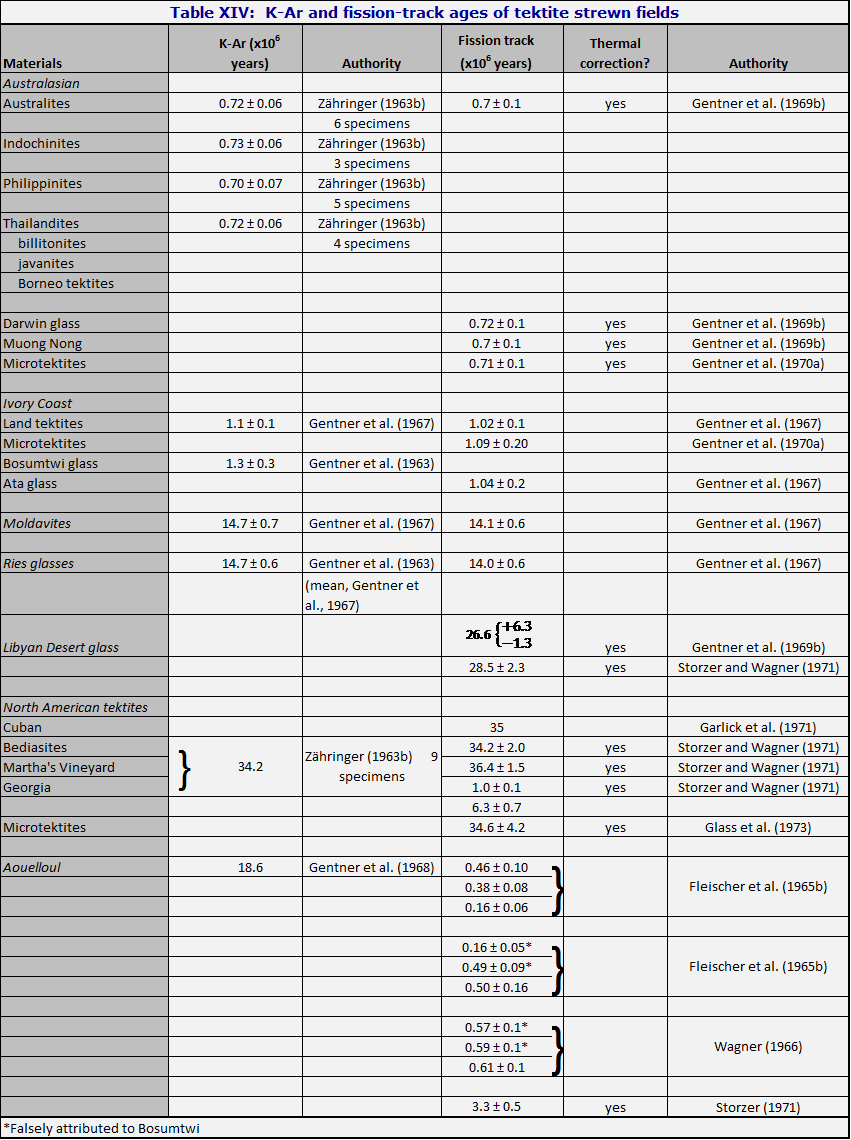
Table XIV gives the K-Ar ages of the principal strewn fields, as well as for some impact glasses whose association with tektites is claimed by some authorities. The good agreement of almost all members of the Australasian strewn field with one another is striking, and had a strong influence on all thinking about the tektite problem. These ages agree well with the ages of the microtektites of the Australasian strewn field, as these have been determined by magnetic stratigraphy and biostratigraphy. In conjunction with the chemical evidence (Chapter 6) they strongly suggest that the Australasian strewn field is a single unit.
Similarly the K-Ar age of the Ivory Coast strewn field is confirmed by the magnetic stratigraphy of the sediments in which the microtektites are found (Glass, 1968); and the K-Ar age of the North American strewn field is confirmed by the stratigraphic age of the North American tektites both on land, where they are found in late Eocene sediments (Jackson), and at sea, where they are reported from sediments of middle Upper Eocene (based on radiolaria) (Glass et al., 1973).
McDougall and Lovering (1969) found K-Ar ages for thirteen australite cores of 0.86 ± 0.06 million years (mean error). The discrepancy with Zähringer's results is perhaps due to the fact that Zähringer did not use a 38Ar tracer; it is not due to any kind of scale error because they found 14.4 million years for a moldavite, inserted as a check. The size of the discrepancy indicates the need for caution; the consistency of the measurements for the Australasian strewn field in Table XIV cannot be used as an indicator of the true errors.
The same authors (1969) also measured ages on the flanges of australites; for six cases they found an age of 1.18 ± 0.28 million years, i.e. older than the cores. The most hopeful explanation of this result, which has been noted (but not published) elsewhere, is that the australites had some inherited argon when they entered the atmosphere; and that this concentrated in the flange. The argon is definitely 40Ar, and therefore did not come from the atmosphere.
Fission-track ages
An entirely independent method of dating the latest heating episode in tektite glass was devised by Fleischer and Price (1964b); it results from the natural fission of 238U. The fission fragments leave damage tracks in the glass which can be detected by etching, followed by optical microscopy. To determine the amount of uranium in the glass, a comparison specimen is bombarded with thermal neutrons, which cause a similar fission of 235U, and thus allow measurement of the uranium content by comparable techniques.
Ages determined in this way are shown in Table XIV, together with the K-Ar ages. It is clear that the two are closely comparable, but a number of interesting new features appear.
In the first place, Gentner et al. (1969b) showed that the fission-track ages of australite flanges are equal, within the errors of measurement, to the ages of the corresponding cores. This point is critical in considering the question of the ages-on-earth of the australites. If the flanges were produced by passage through the atmosphere, which is not seriously questioned by anyone, then these fission-track ages must be the true ages on earth of the australites; they cannot have the ages-on-earth assigned to them by the careful geological studies mentioned in Chapter 2.
In the second place, the Libyan Desert glass can be dated by fission-track methods (the low potassium content makes dificulties for the K-Ar method). This glass was at first believed (Fleischer et al., 1965b) to be simultaneous with North American tektites; but later work (Gentner et al., 1969b) demonstrated that they are some 8 million years younger.
The Darwin glass (Gentner et al., 1969b) was shown to have the same fission-track date as the Australasian strewn field, of which it seems to form part.
The high-sodium tektites discovered by Chapman and Scheiber (1969) were found to have fission-track ages of 4 million years, some five or six times as large as the age of the other Australasian tektites. Since these tektites are similar in shape and in geographic location to other Australasian tektites (though no flanged forms have been found yet) they pose a very serious puzzle. Do they represent a new strewn field? Or can tektites be sent somehow from their source region to the earth without erasure of the fission tracks? If the second alternative is correct, then the source can scarcely be terrestrial meteorite impact; no reservoirs of tektite glass are known and it is not credible that an event of such violence as to fuse tektite glass should leave fission tracks untouched.
It has also been possible to obtain fission-track ages of microtektites from the Australasian strewn field, the Ivory Coast strewn field, and the North American strewn field (Gentner et al., 1970a; Glass et al., 1973). The results confirm the hypothesis that microtektites are genuinely part of the same phenomenon as the land tektites; they also furnish (rather weak) evidence that the Australasian and Ivory Coast strewn fields are really two different events, and not, as Chapman and Scheiber (1969) suggested, parts of the same strewn field.
A persistent problem with the fission-track method is the tendency of the tracks to fade with time. Fleischer and Price (1964c) considered that glass from Clearwater Lake had an age of 33.5 million years, and was related to the North American strewn field. Later, however (Fleischer et al., 1968), the low age was attributed to track fading; the age was revised to 100-300 million years. Methods for correcting for track fading have been brought forward by Storzer and Wagner (1969) and utilized by Gentner et al. (1969b) and Durrani and Khan (1970, 1971a).
Georgia tektites in particular persistently give fission-track ages which are lower than their K-Ar ages, and are inconsistent with each other. They are found apparently weathering out of the mottled clays of the Hawthorne formation; the mottling is due to a patchy local oxidization. Is it possible that the oxidation heats the clay locally, and so causes track fading? An almost identical tektite from Martha's Vineyard, Massachusetts, gives a fission-track age of 35.5 million years (Fleischer et al., 1965b). Even after correcting for track fading, Storzer and Wagner obtained ages ranging from 1.0 to 34 million years for Georgia tektites.
Rubidium-strontium ages
The decay of
87Rb to
87Sr, with a half-life of 60 billion (109) years, also furnishes a way of measuring ages of rocks. In this case, the age is not necessarily the age since the rock was last strongly heated; instead it is the age since the relation of rubidium to strontium was last disturbed. Rubidium, like other alkali elements, tends to concentrate in sialic rocks; hence Rb-Sr ages are ages since the rock was last differentiated.
It is customary to plot the ratios of the isotopes
87Sr/ 86Sr against the ratio of rubidium to strontium (see Fig. 40). For a well-mixed glass which had just been made, there would be a single point giving these two ratios. If now the glass should be differentiated, say by the crystallization and loss of pyroxenes or olivine, so that the alkalis, which are left behind, are concentrated to varying extents in various parts of the melt, then a horizontal line would be produced. It would be horizontal because these chemical processes are expected to change the Rb/Sr ratio, but not (to any measurable extent) the ratio of the two Sr isotopes.
Thereafter, the decay of 87Rb to 87Sr would move the point corresponding to each specimen upward and to the left. (Owing to the long half-life of 87Rb, in comparison with the times here involved, it turns out that the scale needed for 87Sr/ 86Sr runs only from 0.699 to, in most cases, 0.720, while the Rb/Sr ratio ranges by large factors.) Clearly the amount of
87Sr generated is proportional to the amount of
87Rb (and hence to the total Rb) in the original material; on the other hand, the amount of
87Sr is proportional to the total Sr; thus the rate of movement of a point on this graph (as geological time proceeds) is proportional to the Rb/Sr ratio. This converts horizontal initial lines into inclined straight lines. The slope of the straight lines measures the age since differentiation, and its intercept on the axis of
87Sr/
86Sr measures the initial value of this ratio (since with zero Rb this ratio would not change).
When this method is applied to an actual rock or a collection of rocks, one hopes to obtain a more or less linear array capable of being interpreted as described. Two choices are now open for interpreting this diagram.
Isochron age. If the array is convincingly linear, a straight line can be put through the points, and an age, called an isochron age, can be found from the slope of the line. The intercept on the vertical axis yields the initial
87Sr/
86Sr ratio.
Model age. If the array does not appear linear, it may still be possible to extract an age from it, if one can assume a value for the initial
87Sr/
86Sr ratio. Marking this value off on the vertical axis, a line can be drawn through the centroid of the distribution of points; the slope of this line determines what is called a model age
When these methods were first applied to tektites, Pinson et al. (1958) found very low ages -- too low to measure -- assuming an initial
87Sr/
86Sr of 0.712. Later Schnetzler and Pinson (1964b) found that the centroids of the distributions for the three strewn fields which they could then study (the Australasian, moldavite, and bediasite fields) lay on a straight line on the standard plot. The intercept corresponded to
87Sr/
86Sr of 0.7050, and the slope yielded an age of 400 million years.
However, when Schnetzler et al. (1966) measured the Rb-Sr data for the Ivory Coast tektites, they found that the center of the distribution did not fall on the 400-million year isochron defined by the other three strewn fields. Their graph is shown as Fig. 40. Schnetzler et al. also measured the Rb-Sr age of the rocks at the Bosumtwi crater, Ghana; these rocks yielded a very clearcut isochron with an age of 1.97 billion years, and an initial
87Sr/
86Sr of about 0.702.
The age of the Ivory Coast tektites from these data would be about a billion years for the isochron method (though even zero appears to me a possible value; the array is not strongly inclined); the model age falls near 2.5 billion years if the initial value of 87Sr/ 86Sr is near 0.700. Schnetzler et al. noted that the Bosumtwi rock isochron passes through the right-hand end of their distribution. They suggested that all the Ivory Coast tektites had originally lain on the Bosumtwi isochron, but that differential volatilization, occurring during the Bosumtwi impact event, had moved most of the tektites to the left.
This explanation appears to be somewhat ad hoc, although Lippolt and Wasserburg (1966), who also measured the Rb-Sr relations, adopted the same explanation. Schnetzler et al. (1966) supported their ideas by referring to the work of Walter and Carron (1964) on vapor fractionation of tektite melts; these results indicated that rubidium volatilizes rapidly from a melt, like silicon, but more rapidly than strontium. Hence the tektites of lowest silicon ought to be those of lowest Rb/Sr, if volatilization is the correct explanation; and in fact it is found that tektites of high index of refraction (and presumably low silicon) are those of lowest Rb/Sr.
From the physical standpoint, the loss of rubidium (and silica) seems unrealistic. The specimen would surely have to boil, as in the case of argon loss. But in free space it would be expected that boiling would break the object to small pieces, like volcanic ash, or like microtektites. Yet there are Ivory Coast tektites weighing on the order of 100 g.
It is important to see, on the other hand, that in effect both Schnetzler et al. (1966) and Lippolt and Wasserburg (1966) were interpreting the data in terms of an isochron age which is the same as the K-Ar age. This age is the age since the volatilization event, in their theories; but so far as the data go, it could equally well be the age since differentiation.
The moldavite-Ries relation was studied by Philpotts and Pinson (1966) and by Schnetzler et al. (1969). No relation between the Ries and the moldavites was found, in the matter of Rb-Sr abundances. The moldavites showed no measurable correlation of 87Sr/ 86Sr and Rb/Sr over a fairly wide range in Rb/Sr; i.e. the isochron was nearly level. This suggests an age less than 50 million years if straightforwardly interpreted. The authors note the similarity to relations among the Ivory Coast tektites. They suggest a number of hypotheses, including volatilization. The simplest hypothesis is that originally put forward by Pinson et al. (1958), namely that the isochron age is the true age of differentiation. Then the tektites must have formed from a parent magma at some time in the last 50 million years, possibly at the date given by the K-Ar age of 15 million years.
The Rb-Sr relations in the Australasian strewn field were studied by Compston and Chapman (1969). They found that the Rb-Sr relations among Australasian tektites are different for different clans. The high-magnesium clan gives an age of 100 ± 30 million years; the high-calcium clan an age of 265 ± 20 million years. They considered that these results might indicate a number of different igneous suites on the moon; alternatively, the results might indicate meaningless mixtures of lunar volcanics or terrestrial sediments.
The Rb-Sr studies of the North American tektites showed so little spread in Rb/Sr that no isochron could be drawn (Schnetzler and Pinson, 1964b).
The Rb-Sr data taken as a whole indicates clearly that tektites differentiated at dates much more recent than the formation of the moon. If we look at the isochron ages rather than the model ages, it is seen that for many tektite groups ages not far from the K-Ar ages seem to be possible.
Lead-uranium-thorium methods
From examination of lead samples, both terrestrial and meteoritic, it has been found (York and Farquhar, 1972) that it is possible to explain many of them (the conformable leads) by the following discussion:
Theory. When the earth formed, at about -4.55 billion years, the atomic abundances of the isotopes of lead, uranium, and thorium were as shown in Table XV, column 3. The decay of the three radioactive parent nuclides,
232Th,
235U, and
238U, each involves a slowly decaying parent isotope, a number of relatively rapid intermediate radioactive transformations, and a non-radioactive lead isotope at the end. When we are thinking in terms of millions of years, the intermediate steps can be forgotten (the longest, for
234U, is 250,000 years), and we can treat the problem as if the parent nuclides decayed directly into lead.
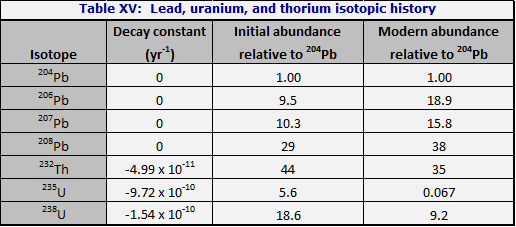
Among the lead isotopes, four are stable. One is non-radiogenic, namely 204Pb. Each of the other three may be formed from a radioactive decay chain; 206Pb from 238U, 207Pb from 235U, and 208Pb from 232Th. It may be useful, in remembering these associations, to note that the two odd isotopes, 207Pb and 235U, are associated; also that the two isotopes with atomic weights divisible by four are associated, namely 232Th and 208Pb. Note also that since one atom of the parent element forms one atom of the final isotope, the sum of the atomic abundances (238U + 206Pb, for example) is constant in time.
These very schematic ideas happen to suffice for dealing with most problems involving tektites; for terrestrial rocks and minerals there are numerous complications, particularly those due to leaching by ground water.
At any time t after the formation of the earth (at -4.55 billion years), the amount of any radioactive isotope, say M, which survives, is given as in (1) by:
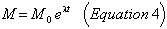
where λ is the decay constant given in column 2 of Table XV, and M0 is the initial abundance of the parent radioactive isotope. The atomic abundance of the corresponding lead isotope, D, is therefore given by:
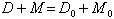
where D0 is the initial abundance of the lead isotope. Then as in (3):
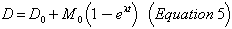
In column 4 of Table XV are the abundances of the relevant isotopes as they are believed to exist in the mantle of the earth today; the lead is common or modern lead.
The very schematic presentation in Table XV does in fact account simultaneously for the lead isotopes in at least some iron meteorites (where there has never been any significant uranium or thorium) and for the abundances of lead isotopes in lead ores, especially galena (PbS) both ancient and recently formed.
Application to tektites in general. Tektite leads are always modern leads, as was first pointed out by Tilton (1958); i.e. the lead isotope abundance ratios are those of column 4 of Table XV. On the other hand, the abundances of uranium and thorium, relative to lead, are not those of column 4, Table XV. Relative to lead, the uranium and thorium are enhanced by factors of 3 to 6. Table XVI was recalculated from Tilton (1958) to put it in the form of Table XV. It is seen at once that while the leads are indistinguishable from modern leads, the uranium is enhanced by a factor of 4, and the thorium by 6.
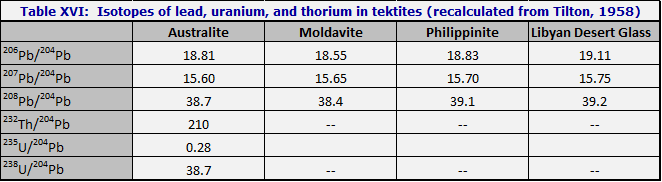
These enhancements are a normal feature of magmatic differentiation, which enhances elements which do not fit easily into the crystal lattices of olivines and pyroxenes. Similar enrichments are seen in most differentiated rocks, especially the more silicic ones.
When did the enhancement occur? One can easily verify by numerical experiments that the differentiation could not have occurred as early as -200 million years; this would have yielded a value of 19.8 for 206Pb/
204Pb. As Tilton remarks, the differentiation process must have taken place in the last 50 million years.
It is also a result of these studies that in all probability tektites are the result of the differentiation of a material very much like the mantle of the earth in its U-Pb-Th ratios.
Starik et al. (1959) analyzed an indochinite, and obtained the startling figures (in units of
204Pb):
206Pb, 28.9;
207Pb, 17.5; and
208Pb, 41.9; these figures imply an age of approximately 4.5 billion years since differentiation. This work may have been in error; in later work (Starik et al., 1961) they found essentially the same result as Tilton: the lead is modern lead, but the uranium is enhanced by a factor of 2 to 5 with respect to the lead. They note that in sedimentary rocks, the Pb/U ratio is usually much greater. The Pb/U ratio in the Libyan Desert glass specimen which they studied approaches the equilibrium value, so that its age of differentiation is not well determined; but the other tektites all have to be young. They concluded (Starik et al., 1962, 1963) that neither igneous rocks nor sedimentary rocks nor meteorites were plausible parents for tektites.
Rowe et al. (1963) measured the thorium contents of tektites, including Libyan Desert glass, which had not been done previously. Rybach and Adams (1969a) measured uranium, thorium, potassium but not lead for Ivory Coast tektites; they found them similar to the Bosumtwi crater glass.
Bosumtwi-Ivory Coast. Wampler et al. (1969) studied the U-Pb relations in the Ivory Coast tektites and Bosumtwi crater glass. For uranium, their results are generally in agreement with Rybach and Adams (1969a) but less consistent. They found that the lead in the Ivory Coast tektites is close to modern lead; but the uranium has been enriched relative to lead by a factor of 3 to 6, as usual; hence it is difficult to understand how tektites could have been differentiated at -2 billion years. One would calculate a value of 24.6 for 206Pb/ 204Pb, for instance. In the Bosumtwi crater glass, they found little enhancement of the U/Pb ratio; here also modern lead was encountered. For the Bosumtwi phyllites (metamorphosed shales), the 238Pb/ 204Pb ratio is 16, rather than 25 or more, as with the tektites. Since the equilibrium value is 9.2, the phyllite data indicate an enrichment of uranium relative to lead of 1.7. The calculated value of 206Pb/ 204Pb after 2 billion years is 21.5; the actual value is 18.0.
The result with the phyllites is clearly an unfortunate coincidence; it is clear that in general it is unusual, in such ancient rocks, to come across lead so modern (cf. the lists of lead isotopes in Russell and Farquhar, 1960). It is probable that the cause of the modern lead in the Ivory Coast tektites is the same as that in all other tektites.
Summary and conclusion from isotopic age dating
Summing up the results of these age studies, let us note that the simplest possible hypothesis does not seem to be excluded, namely that in each strewn field the K-Ar, fission-track, Rb-Sr and lead ages are all telling us about the same event, and all are giving the same ages, within their accuracies. This is the first hypothesis that would be tested for a terrestrial obsidian; since tektites look like obsidians, and were called obsidians by most of the 19th century investigators, it may be that this idea should have priority here also.
It is evidently possible that the lead ages and the K-Ar ages are actually the same. For the Rb-Sr ages, the data for the moldavites directly suggest a very young age; the data for the North American tektites are not in disagreement; and for the Australasian tektites, the high-magnesium group suggests a very low age, though not as low as the K-Ar. For other Australasian tektites, a higher age is suggested; but this may be due to mixing. For the Ivory Coast tektites the same is true.
The stratigraphic age of tektites is usually close to their isotopic age. This suggests that they were thrown from their source region by the same processes, presumably volcanic, as those which reset the isotope clocks and the fission-track clock. The high-sodium tektites would then be an isolated example of material heated and ejected in one eruption, but not then thrown far from the source. They would then have been picked up and launched in the great eruption which produced the Australasian strewn field. If this is right, then a flange of a high-sodium australite might give an age of -700,000 years, while the core gives an age of -4 million years.
ISOTOPIC AND FISSION-TRACK EVIDENCE CONCERNING AGE-IN-SPACE
Age-in-space versus age since last melting
Primary cosmic rays encountering silicates produce a large number of radioactive isotopes, in contrast with the much feebler secondary cosmic ray particles which reach the earth’s surface. Radioactive isotopes produced by primary cosmic rays have been detected in meteorites. They can be distinguished from the so-called naturally radioactive isotopes, which have survived since the formation of the solar system, because the natural radioactivities all have half-lives on the order of 1 billion years or longer, for the obvious reason that those of shorter half-life have already decayed.
Aluminum-26
Ehmann and Kohman (1958a) set up a search for all radioactivities with half-lives less than 109 years. They believed (1958b) that they had found evidence for 26Al (half-life 0.740 million years) and 10Be (half-life 2.7 million years) in the Australasian tektites. Viste and Anders (1962), however, searched for 26Al by looking for the pairs of gamma rays that are produced when the positive electron from 26Al is annihilated by coalescing with a normal electron. Their finding was that the 26Al, if present, was present only at levels much below those found by Ehmann and Kohman. Viste and Anders found an upper limit to the exposure time in space of 90,000 years, provided that the tektites arrived as small, unshielded bodies.
Evidently these calculations are vitiated if the tektites arrived as a single, large body for each strewn field, since in that case the outer parts would shield the inner parts. Viste and Anders calculated that if the radius of the hypothetical large parent body was less than 54 m, then they would have had a fair chance of finding irradiated fragments; this would be about 2 million tons, which Viste and Anders considered to be more than the total mass of the Australasian strewn field. On the other hand, the microtektite data (Glass, 1972a) indicate that the total mass of the Australasian strewn field is near 100 million tons. Thus the validity of the results of Viste and Anders depends on the elimination of the parent-body hypothesis for the origin of tektites.
The microtektite data, however, are probably inconsistent with the arrival of the tektites of a single strewn field in a single mass (O’Keefe, 1969a). It is not possible to explain the wide range of composition in microtektites as a result of ablation from a single parent body. In addition, in order to produce the extensive strewn fields from a single body, it is necessary (O’Keefe and Shute, 1963) to suppose that tektites arrived at a very low angles (less than 3°) to the horizon. But Chapman and his co-workers have produced evidence (see Chapter 3) that in the case of the australites, at least, the descent occurred at relatively steep angles (of the order of 30°), which would exclude arrival as a single body, and would mean that the 26Al measurements do limit the age of tektites in space to less than 90,000 years.
The basic justification for the parent-body hypothesis was originally Urey’s point that if tektites arrive from the moon as a shower of independent bodies, then we must explain why the great majority of tektites, which will surely miss the earth on the first pass, do not go out into orbit, and strike the Earth later. The parent-body hypothesis became superfluous when Paddack (1969) demonstrated that radiation pressure can destroy non-conducting bodies in space by spin-up to rotational bursting (the Radzievskiy-Paddack effect).
Since the Radzievskiy-Paddack effect does not affect large bodies, Cressy et al. (1972) looked for 26Al in the Aouelloul crater glass. The point is that if the hypothetical large glass meteorite had been launched from the moon, it would probably have gone into heliocentric orbit; the crater would then result when the object encountered the earth a million or so years later. The results were negative; in the light of the ages found by Fleischer and Price (1967) of around 0.5 million years, this seemed highly significant. Unfortunately Storzer (1971) revised the track ages of the Aouelloul glass, allowing for track fading, and found 3 million years. Since the half-life of 26Al is 0.74 million years, the 26Al would have fallen to 6% of the initial amount, and would not be detectable.
Neon-21
Reynolds (1960) looked for 21 Ne in tektites. The test is very sensitive; he found that the time of flight must, in the case of some Australasian tektites, have been less than 28,000 years. These results were discounted at first because, as Viste and Anders (1962) remarked, it seemed plausible that tektites might have been outgassed during entry into the earth’s atmosphere; this was especially true on the basis of the parent-body idea. But numerical and physical studies (Chapman, 1964) show that the ablative heating does not penetrate the whole tektite, and the parent-body idea is not needed; thus the test retains its validity. Shielding should be discounted, as noted above.
Neon diffuses out of tektites in a time of the order of a few million years according to the theoretical calculations of Reynolds (1960). These are supported by my previously unpublished observation that neon in tektite vesicles is much less abundant in Australasian tektites than in moldavites (kindly loaned to me by R. Rost) or bediasites. It follows that the 21Ne test does really indicate an age-in-space of less than 28,000 years for the Australasian tektites.
Carbon-14
Boeckl (1972) looked for 14C in some australites. If australites had in fact fallen within the last 20,000 years, and had previously traveled through space for a similar period, then it might have been possible to find 14C; the results were in fact negative.Cosmic ray tracks
Fleischer et al. (1965a) noted that primary cosmic rays passing through tektite glass will produce V-shaped tracks. The primary particle causes fission in nuclei of thorium, uranium, and occasionally lead, while the nucleus is in motion; they are thus distinguishable from the tracks produced by fission when the particle is at rest: in the latter case, the fission fragments must go out in directions precisely opposite.
Cosmogenic tracks have been sought in tektites; they were not found. Fleischer et al. (1965a) showed that, at least in the case of australite buttons, there are regions of the tektite which were never heated enough to erase the tracks. From the total absence of cosmogenic tracks, Fleischer et al. were able to set low limits to the time spent by tektites in space; the maximum flight times ranged from 900 to 6000 years, and include Australasian tektites, an Ivory Coast tektite, a moldavite and a bediasite.
From all these measurements, it is clear that tektites spent at most a few thousand years as separate, unshielded bodies in space.
STABLE ISOTOPES
A few stable isotope abundance ratios, particularly among the lighter elements, can be disturbed by chemical processes. These ratios therefore serve the same function as chemical analyses, in giving some indication of possible relations with other materials.Deuterium/hydrogen
The ratio of deuterium to hydrogen (D/H) was measured by Friedman (1955, 1958). It was found to be similar to that in terrestrial obsidians, ranging from 0.0132 to 0.0166%.Values of D/H are customarily given as δD per mille ( 0/00 ) relative to standard mean ocean water; the relation is:
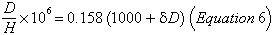
Oxygen isotopes
The relation of 18O to 16O is usually expressed in the form:

Lunar values cluster around +5 to +6 0/00 relative to standard mean ocean water; there are no significant lunar measurements which yield values above +7 (Taylor and Epstein, 1973). On the other hand, all lunar measurements are made on rocks of more or less basaltic composition, except the measures on the silicic part of specimen 12013. On the earth, basaltic rocks give similar values of δ18O. Most silicic igneous rocks give values like tektites. Specimen 12013 (Taylor and Epstein, 1970) gives δ18O in the range +5.9 to +6.5, like the lunar basalts, and not like tektites, nor like terrestrial acid igneous rocks. The specimen is a mixture of silicic and basaltic rock, in close contact (regions a centimeter or so across), so that the possibility arises that the oxygen isotope values resulted from equilibration with the basalt. Taylor and Epstein (1970) consider and reject this possibility, on two grounds:
(1) They consider that most terrestrial granites are metamorphosed sediments; they would therefore expect lunar silicic rock to resemble the rare rhyolitic glasses from oceanic islands, which have δ18O around +5 to +6 0/00 .
(2) They note that the initial values of the 87Sr/86Sr vary from point to point within specimen 12013. This means that the Sr did not equilibrate isotopically; they infer that oxygen would not have equilibrated.
Both arguments are plausible, but neither is compelling. Many students of terrestrial granites think that most granites are not derived from sediments, and hence that the higher δ18O is somehow the result of magmatic differentiation, in which case it might occur on the moon. Second, the diffusion coefficient for oxygen may well be larger than for strontium (personal communication from A.R. Cooper); hence the fact that the strontium isotopes were not equilibrated does not give us assurance that the oxygen isotopes were not equilibrated. They might have been; if they were, then the δ18O may come from the basalt and may not be representative of lunar silicic rocks.
Silicon isotopes
The silicon isotopic ratios were measured by Tilles (1961), in terms of a parameter δ defined by:
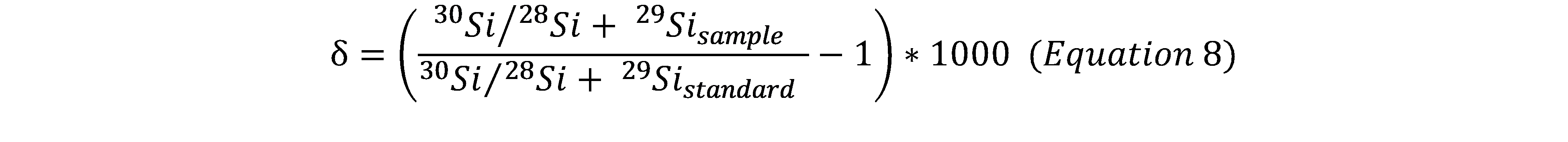
Out of seven measurements, all except one (a bediasite) lay in the range 0 to -31 0/00 relative to a vein quartz standard. The range is small compared to terrestrial sediments, but compares closely to the range in lunar rocks (Taylor and Epstein, 1973).
CONCLUSIONS
From the isotopic data, the following conclusions appear probable:
(1) There are six known tektite strewn fields. In order of age they are: (a) Australasian, age 0.75 million years; (b) Ivory Coast, conceivably identical with (a) age 0.9 million years; (c) Aouelloul, age 3 million years (disputed); (d) Moldavite, age 15 million years; (e) Libyan Desert glass, age 28 million years; and (f) North American strewn field, age 35 million years.
(2) Lead ages of tektites are reconcilable with their K-Ar and fission-track ages. The Rb-Sr ages are not unmistakably inconsistent with the same ages; it is difficult to see why they should not agree with the lead ages, and in some cases, especially the moldavites, they seem to. Conceivably all four ages refer to the same event.
(3) Tektites did not sojourn in space longer than about 900 years.
(4) The D/H ratios in tektites may be consistent with lunar water, at least from the rusty rock (66095).
(5) Oxygen isotope ratios in tektites are generally like those in terrestrial acid igneous rocks. They disagree with the only known lunar acid rock; but the meaning of the disagreement is not clear. Except for Ivory Coast tektites they disagree with most terrestrial sedimentary rocks.
(6) Silicon isotope ratios in tektites are like those in lunar rocks and not like those in terrestrial sedimentary rocks.